Investigación en Educación
Análisis de las pruebas de matemática de la Olimpiada Nacional de Matemática (OLNAMAT – 2017)
Yupay tapukuykuna lakinin yupay suyućhu llallinakuy (OLNAMAT - 2017)
Ayoperotasanoteri oka pruebas de matemáticas de la olimpiada nacional de matemática (OLNAMAT – 2017)
Onesanakengani ora omonkaratanepage ora ogokoitagantsipage kara Omagempitagani timagerontsigitekë ora Ogokoitagantsi(OLNAMAT-2017)
Análise das provas de matemática da Olimpíada Nacional de Matemática (OLNAMAT - 2017)
Analysis of the Mathematics Tests of the National Mathematical Olympiad (OLNAMAT - 2017)
Análisis de las pruebas de matemática de la Olimpiada Nacional de Matemática (OLNAMAT – 2017)
Horizonte de la Ciencia, vol. 12, núm. 22, pp. 271-291, 2022
Universidad Nacional del Centro del Perú

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Recepción: 07 Marzo 2021
Corregido: 14 Julio 2021
Aprobación: 29 Agosto 2021
Resumen: El estudio realizado se encuadra en investigación tipo no experimental, nivel descriptivo; consistió en analizar los resultados y evidencias de los exámenes de matemática que fueron aplicados a los alumnos de Educación Básica Regular (EBR) en la “X Olimpiada Nacional de Matemática (OLNAMAT – 2017)” conducido por estudiantes y profesores de ciencias matemáticas e informática de la Facultad de Educación de la Universidad Nacional del Centro del Perú. Por las condiciones que estamos atravesando (COVID 19) se tuvo como muestra 100 pruebas de educación inicial de 04 y 05 años, determinando la confiabilidad, índice de dificultad, poder discriminativo y coeficiente de validez. El procesamiento cuantitativo de datos es la aplicación de la metodología científica a través de modelos, y el modelo que utiliza son los matemáticos que toman la forma de ecuaciones (psicométricas y edumétricas). Concluyendo que las pruebas pedagógicas de educación inicial de 04 y 05 años tienen α = 0,623 y KR = 0,961, y α = 0,720 y KR = 0,985 respectivamente, es decir tuvo la fiabilidad para su ejecución en la toma de datos; además tienen ambos 5 ítems (33%) caracterizados como “difícil”; 7 ítems (47%) y 10 ítems (67%) representativos por tener “muy buena discriminación”.
Palabras clave: confiabilidad, índice de dificultad, coeficiente de validez, poder discriminativo, prueba pedagógica.
Resumo: O estudo realizado se enquadra em pesquisa do tipo não experimental, nível descritivo; consistiu na análise dos resultados e evidências das provas de matemática que foram aplicadas aos alunos do Ensino Fundamental Regular (EBR) na "X Olimpíada Nacional de Matemática (OLNAMAT - 2017)", realizada por alunos e professores de ciências matemáticas e informáticas da Faculdade de Educação da Universidade Nacional do Centro do Peru. Pelas condições pelas quais estamos passando (COVID 19), foram tomados como amostra 100 testes de escolaridade inicial de 04 e 05 anos, determinando a confiabilidade, índice de dificuldade, poder discriminativo e coeficiente de validade. O processamento de dados quantitativos é a aplicação de metodologia científica por meio de modelos, e o modelo utilizado são os matemáticos que assumem a forma de equações (psicométricas e edumétricas). Concluindo, as provas pedagógicas de formação inicial de 04 e 05 anos possuem α = 0,623 e KR = 0,961, e α = 0,720 e KR = 0,985, respectivamente, ou seja, tiveram a confiabilidade para sua execução na coleta de dados; possuem também ambos 5 itens (33%) caracterizados como "difíceis"; 7 itens (47%) e 10 itens (67%) representativos para “discriminação muito boa”.
Palavras-chave: confiabilidade, índice de dificuldade, coeficiente de validade, poder discriminativo, teste pedagógico.
Abstract: The research carried out is non-experimental and descriptive level; It consisted of analyzing the results of the mathematics tests that were applied to the students of Regular Basic Education (RBE) in the "10th National Mathematical Olympiad (OLNAMAT - 2017)" conducted by students and professors of the PAS Mathematical Sciences and Information Technology of the Faculty of Education of the National University of Central Peru. A sample of 100 mathematics tests for initial education of 04 and 05 years was taken, determining their reliability, difficulty index, discriminative power and validity coefficient. Statistical methodology was applied for quantitative data processing and some of the psychometric and edumetric statistics were calculated. Concluding that the mathematics tests for initial education of 04 and 05 years have α = 0,623 and KR = 0,961, and α = 0,720 and KR = 0,985, respectively; that is, they are reliable for data collection; furthermore, the tests have 5 items (33%) and 7 items (47%), characterized as "difficult"; respectively, as well as 10 items (67%) with “very good discrimination”.
Keywords: reliability, difficulty index, validity coefficient, discriminative power, pedagogical test.
Introducción
En la última evaluación internacional PISA 2018, en el Perú se evaluó a 8208 escolares de 342 instituciones educativas públicas y privadas, entre los días 14 de agosto y 30 de setiembre, siendo desarrollada usando los ordenadores; debemos mencionar que PISA, primordialmente es una de las evaluaciones internacionales que explora las competencias de matemática, lectura, ciencia y educación financiera en alumnos de 15 años que están por acabar la educación secundaria; además Perú participó voluntariamente en los años 2000, 2009, 2012, 2015 y 2018.
Siendo de importancia para nuestro estudio las competencias evaluadas en el área de matemática, como son: “cambio y relaciones, espacio y forma, cantidad e incertidumbre y datos; procesos tales como: formular situaciones matemáticamente, emplear conceptos, hechos, procedimientos y razonamientos matemáticos, e interpretar, aplicar y evaluar los resultados matemáticos” (MINEDU; 2019). Resultados
| País | 2009 | 2012 | 2015 | 2018 | Variación 2009-2012 | Variación 2012-2015 | Variación 2015-2018 | Tendencia promedio 2009-2018 |
| Perú | 365 | 368 | 387 | 400 | +3,0 | +18,5 | +13,3 | +11,7 |
| Colombia | 381 | 376 | 390 | 391 | -4,4 | +13,2 | +1,3 | +3,3 |
| Brasil | 386 | 389 | 377 | 384 | +2,7 | -11,4 | +6,5 | -0,7 |
| …. |
Observamos la tendencia de nuestros estudiantes un crecimiento de los puntajes significativamente con una probabilidad del 0,05, y los escolares de los colegios privados logran como media aritmética 60 puntos al igual que sus pares de las instituciones públicas, sin embargo, cuando se consideran las características socioeconómicas de los alumnos, esta diferencia se reduce a 14 puntos.
A nivel nacional son diferentes las instituciones que organizan eventos “concursos” en las áreas básicas, siendo una de ellas las matemáticas, cuyos propósitos son: fomentar y propagar el aprendizaje de la matemática en los alumnos de EBR, valorando su importancia en el desarrollo del país, y estimular la investigación y la creatividad en la enseñanza de la matemática. Tenemos:
Ø Concurso Nacional de Matemática (CONAMAT), auspicia la Universidad de Ciencias y Humanidades
Ø Olimpiada Nacional Escolar de Matemáticas (ONEM), auspicia el Ministerio de Educación a través del Sistema de información de participantes para los concursos educativos (SICE).
Ø Olimpiadas de Matemáticas, auspicia la Academia Trilce.
Ø Olimpiada Nacional de Matemática (OLNAMAT), auspicia la Universidad Nacional del Centro del Perú.
Ø Concurso Interescolar de Matemáticas, auspicia la Universidad Nacional de Trujillo.
Ø Concurso Escolar de Matemáticas, auspicia el consorcio Saco Oliveros.
El Ministerio de Educación a través de la Unidad de Medición de la Calidad, recomienda, “impulsar la especialización de los docentes del II y III Ciclo de EBR en la enseñanza de la lecto escritura y de matemática de manera que éstos puedan contar con un mejor conocimiento conceptual y metodológico de los procesos de enseñanza aprendizaje en estas dos áreas” (MINEDU, 2019).
Si ahondamos históricamente en las raíces de los principales resultados matemáticos llegaremos siempre a preguntas relacionadas con el mundo real, con el comportamiento de la naturaleza. Para explicar o generalizar algunas de las propiedades observadas en el mundo real, los matemáticos desarrollan conceptos y definen estructuras matemáticas abstractas (por ejemplo, la noción de grupo, la noción de matriz). Para un matemático las estructuras abstractas tienen una realidad propia, y el matemático las investiga sistemáticamente, casi como un biólogo investigaría un animal. En pocas palabras, “las matemáticas son una ciencia como cualquier otra (la biología o la física), con la ventaja de que los resultados que se demuestran en esta ciencia son verdades universales que no dependen del tiempo o de los gustos de los hombres”, (Peña; 2017; p.158).
OEI (2015) “se aprende matemática haciendo matemática, realizando una mirada transversal a los distintos contenidos que se abordan a lo largo de la escolaridad secundaria y a lo largo de toda la escolaridad en general) se observa que algunos de estos haceres se repiten en muchos de los contenidos, variando sutilmente de uno a otro”. La evaluación de las pruebas objetivas de matemática se administra en diferentes situaciones explícitas o implícitas, encontrándose al interior la medición normalizada o prueba estándar. De modo que estas pruebas permitirían verificar los logros académicos de los niñ@s en la comprensión lectora concordante a su grado de estudio y edad respectivamente. De la misma manera los productos señalarían las destrezas que los escolares dominan, como también de las que tienen conflictos, en suma con estas comunicaciones se aceptarían medidas para mejorar estas habilidades ligados con la matemática.
Siendo el problema general: ¿Cuáles son los índices numéricos para la confiabilidad, coeficiente de validez, índice de dificultad y poder discriminativo de las pruebas objetivas de matemática en la “X Olimpiada Nacional de Matemática – UNCP – 2017”?, así mismo los problemas específicos son: a) ¿Cuáles son los índices numéricos para la confiabilidad, coeficiente de validez, índice de dificultad y poder discriminativo de las pruebas objetivas de matemática, en educación inicial de cinco años, de la “X Olimpiada Nacional de Matemática – UNCP – 2017”? y b) ¿Cuáles son los índices numéricos para la confiabilidad, coeficiente de validez, índice de dificultad y poder discriminativo de las pruebas objetivas de matemática, en educación inicial de cuatro años, de la “X Olimpiada Nacional de Matemática – UNCP – 2017”?
El objetivo general fue: Determinar y describir los índice numéricos para la confiabilidad, coeficiente de validez, índice de dificultad y poder discriminativo de las pruebas objetivas de matemática de la “X Olimpiada Nacional de Matemática – UNCP – 2017”, y los objetivos específicos son: a) Calcular y describir los índices numéricos para la confiabilidad, coeficiente de validez, índice de dificultad y poder discriminativo de las pruebas objetivas de matemática, en educación inicial de cinco años, de la “X Olimpiada Nacional de Matemática – UNCP – 2017”, y b) Calcular y describir los índices numéricos para la confiabilidad, coeficiente de validez, índice de dificultad y poder discriminativo de las pruebas objetivas de matemática, en educación inicial de cuatro años, de la “X Olimpiada Nacional de Matemática – UNCP – 2017.
En la actualidad se utilizan diversos instrumentos de evaluación que intentan medir los aprendizajes de la matemática y la resolución de problemas a través de pruebas objetivas de matemática de los estudiantes de EBR de la provincia de Huancayo de la región Junín, a través de los concursos de matemática. Las pruebas suministradas en esta área complicada, reinciden en los resultados como una clasificación discriminatoria, manifestándose la disconformidad entre las organizaciones educativas de las regiones. Pese a lo cual, se advierte la carencia de validación y confiabilidad de las pruebas objetivas utilizadas para este fin; asimismo la aplicación de los contenidos en el contexto y conseguir la referencia para poder asistir individualmente a aquellos estudiantes que participan y no entienden.
No cabe ninguna dubitación de lo complicado que entraña el grado de medición en la resolución de problemas, a través de los concursos de matemática, la cognición sobre las cualidades interactivas en el desarrollo de la solución del problema impide obtener una respuesta fácil, la intención de ordenar las estrategias o habilidades conllevaron a un fracaso, asimismo el entendimiento o conversión de la expresión verbal en el lenguaje matemático manifiesta la debilidad de la comprensión lectora, “hacen que el estudiante confunda la representación propuesta con el concepto matemático que quiere aprender (en ocasiones esta situación se presenta en el docente mismo)” D’Amore, Fandiño, Marazzani y Sbaragli (2011; p.91).
Considerando la importancia que tiene la evaluación de la resolución de problemas en la formación escolar, siendo uno de los pilares en el logro de aprendizaje de la matemática; “estar matemáticamente alfabetizado implica evidenciar un buen dominio de las capacidades de analizar, razonar y comunicar eficazmente al enunciar, formular y resolver problemas matemáticos” (OCDE; 2003; p.46).
El presente estudio tiene como finalidad fundamental, analizar el coeficiente correlacional de la validación y confiabilización de los exámenes de matemática de los estudiantes de EBR de la provincia de Huancayo de la región Junín, a través de los concursos de matemática, que llegando hacer consistente y coherente servirá como un instrumento de parámetro para evaluar esta complicada capacidad, de tal manera que ayude a los profesores y estudiantes.
Macías (2011) desarrolló el trabajo de investigación: “Validación y confiabilidad de pruebas de opción múltiple para la evaluación de habilidades”. Concluye la validez y confianza se objetiviza en el resultado del examen de geografía, tipo opción múltiple, a través de la calidad evaluativa, potencializando las capacidades logradas y la facilidad del suministro a los estudiantes.
Jara (2015) desarrolló el estudio: “Validez y confiabilidad en la construcción de reactivos utilizados en pruebas de opción múltiple (POM)”. Concluye la manipulación estratégica de los distractores (psicológica y pedagógica), justifica cognitivamente la medición de un contenido; siendo beneficioso la realización de una muestra de pruebas para demostrar la validez y confiabilidad del formato de POM. El objetivo de elaborar los reactivos en una POM no necesariamente deben ser complejos, pues estos solo nos ayudan a rescatar los conocimientos que deben tener nuestros estudiantes con los temas impartidos en clase (p. 13).
Álvarez (2018) desarrolló la pesquisa: “Validación del instrumento de conocimientos sobre técnicas de manejo de conducta no farmacológicas en estudiantes del internado de la Universidad Alas Peruanas 2017”. Investigación observacional, prospectiva, descriptiva y transversal; trabajó con 6 especialistas “expertos” para la evaluación de la encuesta, con 30 internistas para la validez de contenido y 80 alumnos para la validez de constructo, siendo calculados los índices con la “V de Aiken”, “Análisis factorial” y el “Alpha de Cronbach”. Concluye que la validez de contenido tiene un índice de 0,98; la reproductibilidad de 0,89; la validez de constructo tiene 0,43 y las técnicas de distracción y contingente tiene 0,77; en forma general el instrumento tiene 0,76 de confiabilidad.
Cárdenas (2013) desarrolla la investigación “Dificultad y sensibilidad de los instrumentos de recolección de datos”. Investigación aplicada, nivel descriptivo correlacional; concluyendo que existe correlación causa-efecto entre la simetría (facilidad-dificultad) y la curtosis (grado de sensibilidad), de los instrumentos de acopio de datos: un cuestionario, dos fichas de observación, seis pruebas pedagógicas (2 politómicas y 4 dicotómicas).
Validez y confiabilidad de los instrumentos de recolección
En el desarrollo de la recogida de datos, es indispensable el uso de diversos instrumentos relacionados a las técnicas perceptivas (observación), entrevista, encuesta, procesos experimentales; es por ello que, de una u otra forma, se estaría desarrollando la evaluación de las variables. La veracidad de la data en la organización de la información, base imprescindible de obtener resultados y de ello proyectar el análisis correspondiente en la investigación. “En cualquier supuesto en el que sea necesario construir una prueba y, por lo tanto, conocer la fiabilidad de esa prueba, se tiene que tener en cuenta el tipo de prueba, la forma de obtener las medidas repetidas, las condiciones de aplicación, etc.” (Santisteban; 2009; p.90).
Siendo inevitable que los instrumentos, deberían tener índices de validación y confiabilización; de tal manera, aseverar que las pruebas pedagógicas sean oportunas, apropiadas y convenientes para el logro de los objetivos de la recopilación de los datos, fenómeno de investigación, en forma general todo instrumento debería tener la validez y confiabilidad de jueces o expertos y pequeños grupos. “La elaboración de una técnica psicométrica es un proceso que lleva mucho tiempo, paciencia y dedicación. Los mejores resultados se obtienen con el trabajo en equipo y varios ensayos en muestras piloto, todos los que sean necesarios para depurar el instrumento” (Fernández, Cayssials y Pérez; 2009; p.158), en particular al evaluar el aprendizaje de la matemática a través de los concursos de conocimientos referente al área.
Validez.- La definición más común sobre el concepto de validez señala el grado en que el instrumento mide la variable que pretende medir. Es decir, al interpretar los resultados del instrumento, en realidad puede afirmarse que estos son una prueba de las condiciones del individuo o del fenómeno evaluado. Por ejemplo, “un método para medir el rendimiento bursátil tiene que medir precisamente esto y no la imagen de una empresa”, “una prueba sobre conocimiento de historia tiene que medir esto y no conocimientos de literatura histórica”, etc. La validez, a su vez, puede dividirse en:
Ø Validez de facie o aparente: Se refiere a cierta demostración empírica de que una prueba mide lo que dice medir. Se da a partir del hecho de que un instrumento “parece” medir las variables elegidas para un estudio.
Ø Validez de contenido: Se refiere al grado en que un instrumento refleja un dominio específico de contenido de lo que se mide. Esto es, si la prueba contiene suficientes elementos, preguntas o ítems para decirse que con ello es factible recoger la información necesaria. Y además si el número de los elementos del instrumentos abarcan los distintos componentes del fenómeno que se investiga. Se busca saber si el instrumento mide adecuadamente las principales dimensiones de la variable en cuestión.
Ø Validez de constructo: Es probablemente el parámetro más importante que debe cumplir un instrumento, ya que esta se refiere al hecho de que el instrumento mida un concepto teórico. Es decir, se buscará que exista claridad sobre lo que se mide, de modo que las preguntas estén directamente relacionadas con el asunto a medir. Un constructo, como se explicara antes, es una variable medida que tiene lugar dentro de una hipótesis.
Ø Validez de criterio: Establece la validez de un instrumento al compararla con algún criterio externo que pretende medir lo mismo. Cuanto más se relacionen los resultados del instrumento con el criterio, la validez será mayor. En la validez de criterio predictiva, la prueba buscará pronosticar la condición de algún criterio a la que se llegará en el futuro. Mientras que la validez de criterio concurrente se revisa por la concordancia entre los resultados del instrumento y la condición actual de los sujetos. Estos conceptos de validez y confiabilidad son aplicables tanto a instrumentos usados en una investigación de enfoque cualitativo, como a estudios de enfoque cuantitativos o mixtos.
Confiabilidad. Es un indicador de cualidad de los procedimientos evaluativos, sinónimo de credibilidad, certidumbre o seguridad. “Un instrumento es confiable cuando los valores obtenidos para una determinada característica son iguales en sucesivas aplicaciones, siempre que las condiciones en que se den, sean iguales” Encinas (1987; p.44).
Un instrumento tiene fiabilidad dimensionalmente de la coherencia que existe en los mismos resultados o puntuaciones obtenidas en el caso de un sujeto, la medición puede duplicarse o proliferarse con cierta exactitud; como también la confiabilización del instrumento debería ser causa de similar percepción y evaluación. “En la medida en que los errores de medición estén presentes en un instrumento de medición, en esa misma medida el instrumento es desconfiable. La confiabilidad puede definirse como la ausencia relativa de errores de medición en un instrumento” Kerlinger (1994; p.459). Para calcular el índice de confiabilidad, mencionamos algunos métodos:
Ø Test-retest.- La fiabilidad por este método es evaluar la relación entre las puntuaciones de un instrumento en un intervalo de tiempo, “sobre la confiabilidad de las puntuaciones…, por el método test-retest…, el intervalo [de tiempo] no sea muy prolongado ni muy corto y separe ambas administraciones con intervalo cuatro meses” Fernández et al (2009; p.131).
Ø División en dos partes iguales.- Conocido también como método Split-Halves, se correlaciona los datos (puntuaciones) del test dividido en partes iguales. “En un test con ítems muy homogéneos, cualquier división en dos partes iguales se puede aceptar como adecuada” Santisteban (2009; p. 85). Otra manera muy usada en un “test de aptitudes”, consiste en seleccionar los ítems pares e impares y su cálculo es mediante la correlación por rangos o correlación de Spearman.
Ø Formas paralelas.- La confiabilización mediante este método es de dos instrumentos elaborados de forma paralela. Las formas paralelas de los test deberían ser idénticos o análogos en contenido, instrucción y temporalización en el suministro del test; es decir, se diseñan dos instrumentos en las mismas condiciones y su aplicación es en el mismo momento.
Ø Entre calificadores o entre jueces.- Este método consiste en la relación de las puntuaciones o anotaciones de dos o más “jueces o expertos” al instrumento suministrado, verificando su consistencia.
Factores que determinan la falta de confiabilidad. Si bien son múltiples las causas por las cuales los puntajes obtenidos por un evaluado pueden no ser confiables, sintetizaremos solamente algunas fuentes de error:
Ø Al construir o adaptar una prueba objetiva: se debe prestar atención a la selección de los ítems y a la formulación de las consignas, pero principalmente se debe cuidar el muestreo del contenido para evitar que sea tendencioso o insuficiente. Otra fuente importante de error son los efectos de la adivinación, es decir, los tests son más confiables a medida que aumenta el número de respuestas alternativas (Cantorin, 2014).
Ø Al administrar un test: se debe evaluar a todos los sujetos en las mismas condiciones, tratando de controlar posibles interferencias ambientales como el ruido, la iluminación o el confort del lugar. Las consignas deberían ser estandarizadas desde la construcción del test hasta en su administración, especialmente en lo referido al control de los tiempos para la realización del mismo. Otro punto a considerar son las influencias fortuitas que pueden afectar la motivación o la atención del evaluado como por ejemplo preocupaciones personales, afecciones físicas transitorias, etc.
Ø Al evaluar un test: se deben sostener los criterios de evaluación, no es posible cambiar los criterios de corrección por ejemplo luego de haber calificado a una serie de evaluados, en función de un criterio subjetivo del evaluador.
Materiales y métodos
Tipo de investigación no experimental porque se analizó la confiabilidad y validez de las pruebas de matemática de la “X Olimpiada Nacional de Matemática – UNCP – 2017”, de la Facultad de Educación de la Universidad Nacional del Centro del Perú.
Nivel descriptivo, porque se describen las pruebas de matemática de la “X Olimpiada Nacional de Matemática – UNCP – 2017”, de la Facultad de Educación de la Universidad Nacional del Centro del Perú. “Además de la preparación de los maestros, (Labaree; 2004; p.12) afirma que las escuelas de educación son responsables de la producción de la investigación educativa”.
Se utilizó el método científico y el método descriptivo. El índice estadístico de confiabilidad, validez, índice de dificultad, coeficiente de validez y poder discriminativo de las pruebas de matemática es consistente y coherente para medir el nivel de aprendizaje de los niñ@s de cuatro y cinco años.
El diseño que se utilizó es el descriptivo simple cuyo esquema es:
M. --------------- O.
M. --------------- O.
Donde:
M. y M., representan las muestras
O. y O., representan la información
Variable de estudio. Prueba de matemática de la “X Olimpiada Nacional de Matemática – UNCP – 2017”, de la Facultad de Educación de la Universidad Nacional del Centro del Perú.
Población. Son las pruebas de matemática de los niveles de educación inicial, primaria y secundaria de EBR.
Muestra. El marco muestral se eligió a través del muestreo al azar, obteniendo 100 pruebas de educación inicial (50 de cuatro años y 50 de cinco años).
Técnicas e instrumentos de investigación
a) La observación: Esta técnica se utilizó para identificar en la resolución de problemas el índice de dificultad y el poder discriminativo.
b) El fichaje: Mediante esta técnica se recogió de manera ordenada y sistemática todo tipo de información bibliográfica, referida a los aspectos teóricos conceptuales de la investigación.
Los instrumentos que se emplearán serán las pruebas de matemática de la “X Olimpiada Nacional de Matemática – UNCP – 2017”.
Resultados
| Estadísticos | 4 años | 5 años |
| Promedio | 08 | 09 |
| Mediana | 09 | 08 |
| Moda | 11 | 08 |
| Varianza | 12,91 | 11,65 |
| Desviación estándar | 3,59 | 3,41 |
| Coef. Variación | 42% | 38% |
| Coef. Asimetría | -0,14 | 0,13 |
| Kurtosis | -0,39 | -0,73 |
Con respecto al promedio la muestra de 4 años tiene 08 y la de cinco años 09, existiendo una diferencia de un punto, asimismo para la mediana se tiene 09 y 08 respectivamente, ambos son unimodales con 11 y 08 de puntuación respectivos.
Las puntuaciones obtenidas con los estadígrafos de dispersión (04 años y 05 años) son las siguientes: Varianza 12,91 y 11,65, desviación estándar 3,59 y 3,41, y el coeficiente de variación 42% y 38%, es decir es heterogénea las puntuaciones en ambos grupos.
Y por último con los estadígrafos de forma se tiene con el coeficiente de asimetría comentarios opuestos porque para la prueba de 04 años (As = -0,14) sesgo negativo y examen fácil, mientras que para la prueba de 05 años (As = 0,13) sesgo positivo y examen difícil. Con respecto a la kurtosis el apuntamiento de la curva normal es platicúrtica para ambos grupos (-0,39 y -0,73)
| Técnicas | 4 años | 5 años |
| Alpha de Cronbach | 0,6228 | 0,7204 |
| Kuder-Richardson | 0,9612 | 0,9854 |
La fiabilidad de los exámenes con el Alpha de Cronbach son: 0,6228 y 0,7204 y con Kuder-Richardson: 0,9612 y 0,9854 respectivamente.
| Criterios | 4 años | 5 años | ||
| No. | % | No | % | |
| Muy fácil | 2 | 13% | 3 | 20% |
| Fácil | 3 | 20% | 3 | 20% |
| Intermedio | 1 | 7% | 1 | 7% |
| Difícil | 5 | 33% | 5 | 33% |
| Muy difícil | 4 | 27% | 3 | 20% |
| Total | 15 | 100% | 15 | 100% |
Observamos en el índice de dificultad la predominancia de preguntas difíciles en ambos grupos con 33% y con respecto al menor porcentaje 7% se ve con la pregunta de criterio intermedio.
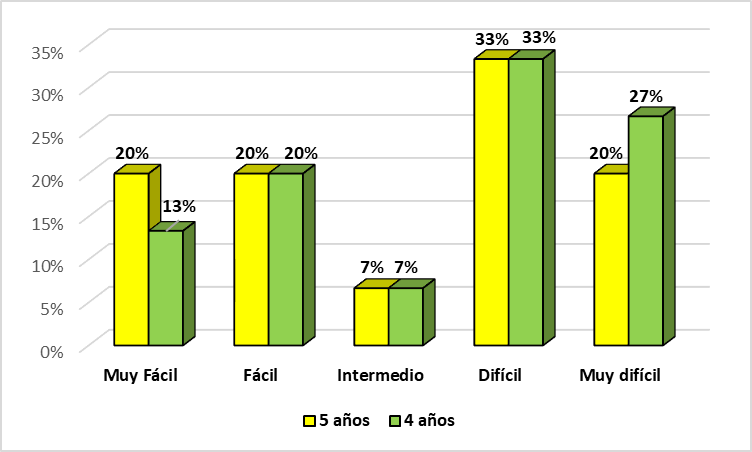
Figura 1
Índice de dificultad
| Criterios | 4 años | 5 años | ||
| No. | % | No | % | |
| Baja discriminación | 4 | 27% | 1 | 7% |
| Buena discriminación | 4 | 27% | 4 | 27% |
| Muy buena discriminación | 7 | 47% | 10 | 67% |
| Total | 15 | 100% | 15 | 100% |
Prevalece “muy buena discriminación” en ambas pruebas de 04 años (47%) y 05 años (67%), además en el criterio “buena discriminación” ambos exámenes tienen el mismo porcentaje (27%).
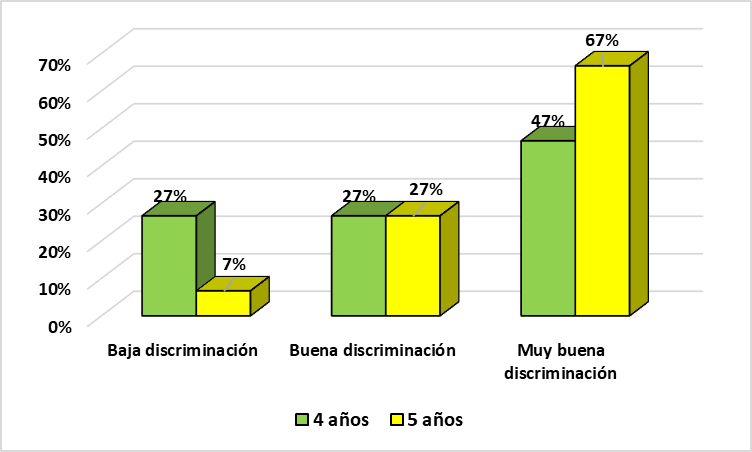
Figura 2
Poder discriminativo.
Aspectos descriptivos de la prueba escrita de 04 años
| Estadígrafos FactorComentario Coeficiente de validez 0,39 Válido Índice de dificultad 0,38 Difícil Poder discriminativo 0,44 Muy buena discriminación |
| Estadígrafos FactorComentario Coeficiente de validez 0,32 Válido Índice de dificultad 0,60 Fácil Poder discriminativo 0,36 Buena discriminación |
| Estadígrafos FactorComentario Coeficiente de validez 0,24 Válido Índice de dificultad 0,18 Muy difícil Poder discriminativo 0,28 Baja discriminación |
| Estadígrafos FactorComentario Coeficiente de validez 0,26 Válido Índice de dificultad 0,18 Muy difícil Poder discriminativo 0,30 Buena discriminación |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,22 “Válido” “Índice de dificultad” 0,82 “Muy fácil” “Poder discriminativo” 0,26 “Baja discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,35 “Válido” “Índice de dificultad” 0,40 “Difícil” “Poder discriminativo” 0,40 “Muy buena discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,22 “Válido” “Índice de dificultad” 0,32 “Difícil” “Poder discriminativo” 0,26 “Baja discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,38 “Válido” “Índice de dificultad” 0,76 “Muy fácil” “Poder discriminativo” 0,35 “Buena discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,47 “Válido” “Índice de dificultad” 0,50 “Intermedio” “Poder discriminativo” 0,53 “Muy buena discriminación |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,47 “Válido” “Índice de dificultad” 0,28 “Difícil” “Poder discriminativo” 0,53 “Muy buena discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,38 “Válido” “Índice de dificultad” 0,24 “Muy difícil” “Poder discriminativo” 0,44 “Muy buena discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,23 “Válido” “Índice de dificultad” 0,14 “Muy difícil” “Poder discriminativo” 0,27 “Baja discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,23 “Válido” “Índice de dificultad” 0,14 “Muy difícil” “Poder discriminativo” 0,27 “Baja discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,46 “Válido” “Índice de dificultad” 0,72 “Fácil” “Poder discriminativo” 0,51 “Muy buena discriminación” |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,49 “Válido” “Índice de dificultad” 0,66 “Fácil” “Poder discriminativo” 0,54 “Muy buena discriminación” |
Se tiene para la prueba escrita de 05 años
| Estadígrafos FactorComentario Coeficiente de validez 0,43 Válido Índice de dificultad 0,88 Muy fácil Poder discriminativo 0,49 Muy buena discriminación |
| Estadígrafos FactorComentario Coeficiente de validez 0,43 Válido Índice de dificultad 0,88 Muy fácil Poder discriminativo 0,49 Muy buena discriminación |
| Estadígrafos FactorComentario Coeficiente de validez 0,48 Válido Índice de dificultad 0,32 Difícil Poder discriminativo 0,53 Muy buena discriminación |
| Estadígrafos FactorComentario Coeficiente de validez 0,30 Válido Índice de dificultad 0,76 Muy fácil Poder discriminativo 0,35 Buena discriminación |
| Estadígrafos FactorComentario “Coeficiente de validez” 0,43 “Válido” “Índice de dificultad” 0,66 “Fácil” “Poder discriminativo” 0,48 “Muy buena discriminación” |
Discusión
En el año 2011 Macías admite en los resultados de una prueba de opción múltiple de geografía, la validación y confiabilización permitiéndole un mejor logro de aprendizaje; mientras los resultados evaluados en las pruebas de matemática en el nivel inicial de 4 y 5 años no permiten una visualización objetiva del logro de las capacidades, sería por el tipo de respuestas (abiertas) o la caracterización de una prueba difícil, por ello el promedio desaprobatorio.
La confiabilidad obtenida en los exámenes a través del Alpha de Cronbach son 0,6228 y 0,7204 fiables por la convencionalidad (α > 0,60), si nos ceñimos estrictamente para Cronbach donde α > 0,80, ambas pruebas de matemática del nivel inicial de 4 años y 5 años no serían confiables. Pero Jara (2015) justifica cognitivamente la medición de un contenido mediante una muestra de pruebas para demostrar la validez y confiabilidad en el formato de “pruebas de opción múltiple” (POM); mientras que Álvarez (2018) trabajó con 6 especialistas “expertos” para la evaluación de la encuesta, con 30 internistas para la validez de contenido y 80 estudiantes para la validez de constructo.
Conclusiones
La confiabilidad de las pruebas de matemática, nivel inicial de 4 y 5 años, de la OLNAMAT-2017 se dieron a través del Alpha de Cronbach (α4 años = 0,6228 y α5 años = 0,7204), Kuder-Richardson (KR4 años = 0,9612 y KR5 años = 0,9854), todos los ítems validos determinados con el coeficiente de validez, además un porcentaje mayoritario ítems “difíciles” y “muy buena discriminación” mediante el poder discriminativo para una prueba pedagógica.
La confiabilidad de la prueba de matemática, nivel inicial de 04 años, de la OLNAMAT-2017 se dieron a través del Alpha de Cronbach (0,6228), Kuder-Richardson (0,9612), los quince (15) ítems validos determinados con el coeficiente de validez, además porcentaje mayoritario ítems “difíciles” (33%) e ítems “muy difíciles” (27%); “muy buena discriminación” (47%), “buena discriminación” y “baja discriminación” ambos con 27% determinados mediante el poder discriminativo.
La confiabilidad de la prueba de matemática, nivel inicial de 05 años, de la OLNAMAT-2017 se dieron a través del Alpha de Cronbach (0,7204), Kuder-Richardson (0,9854), los quince (15) ítems validos determinados con el coeficiente de validez, además porcentaje mayoritario ítems “difíciles” (47%) y los ítems “muy difíciles”, “fácil” y “muy fácil” (20%); “muy buena discriminación” (67%), “buena discriminación” (27%) y “baja discriminación” (7%) determinados mediante el poder discriminativo.
Recomendaciones
Antes de aplicar un instrumento, se recomienda la revisión por los “expertos” y validado por los “pequeños grupos”, porque la validez de un diseño de investigación se refiere al grado de control y posición de generalización que tiene el investigador sobre los resultados obtenidos. Los diseños de investigación deben tener dos tipos de validez: validez interna y validez externa.
Para la selección de la muestra debe utilizarse la técnica de “selección diferencial de los sujetos”, es decir este factor ocurre cuando el investigador selecciona a las personas del grupo a su criterio, y no en forma aleatoria, como debería ser al formar los grupos de investigación, debe utilizarse los procedimientos de asignación aleatoria o apareamiento aleatorio.
Referencias
Álvarez, K. (2018). Validación del instrumento de conocimientos sobre técnicas de manejo de conductas no farmacológicas em estudiantes del internado de la Universidad Alas Peruanas 2017. Tesis. Lima: Universidad Alas Peruanas.
Cantorin, R. (2014). Técnicas de procesamiento de datos e información utilizando Excel. (Trabajo de investigación). Huancayo: Talleres de Gráficas Inversiones M&C.
Cárdenas, A. (2013). Dificultad y sensibilidad de los instrumentos de recolección de datos. Trabajo de investigación. Huancayo: Editora Imprenta Ríos SAC.
D’Amore, B., Fandiño, M., Marazzani, I. y Sbaragli, S. (2011). La didáctica y la dificultad en matemática. Análisis de situaciones con falta de aprendizaje. (2ª ed.) Bogota, D. C. Colombia: Cooperativa Editorial Magisterio.
Encinas, I. (1987). Teoría y técnicas en la investigación educacional. Lima: AVE S.A.
Fernández, M., Cayssials, A. y Pérez, M. (2009). Curso básico de psicometría. Teoría clásica. Buenos Aires: Lugar Editorial.
Jara, M. (2015). Validez y confiabilidad en la construcción de reactivos utilizados en pruebas de opción múltiple (POM). Artículo Científico. Puno: Universidad Andina Néstor Cáceres Velásquez.
Kerlinger, F. (1994). Investigación del comportamiento. (3ª Edición en inglés y 2ª Edición en Español). México D. F.: McGraw-Hill.
Labaree, D. (2004). The trouble with ed schools. New Haven: Yale University Press.
Macías, E. (2011). Validación y confiabilidad de pruebas de opción múltiple para la evaluación de habilidades. (Tesis de maestria). CIMAT. Guanajuato: Centro de investigación en Matemáticas, A. C.
MINEDU - Ministerio de Educación del Perú (2019). Resultados PISA-2018. En http://umc.minedu.gob.pe/resultadospisa2018.
OCDE (2003). Alfabetización en matemáticas y ciencias. Recuperado el 24 de noviembre de 2020. En http://www7.uc.cl/sw_educ/educacion/grecia/plano/html/pdfs/biblioteca/LIBROS/BL011.pdf
OEI - Organización de Estados Iberoamericanos (2015). La evaluación en el área de matemática. Claves y criterios. Nivel secundario. Buenos Aires: OEI. Directores que hacen escuela.
Peña, J. (2007). Álgebraen todas las partes. (3ra. Reimpresión). México: La Ciencia para todos/166. Fondo de Cultura Económica.
Santisteban, R. (2009). Principios de psicometría. España: Síntesis S. A.
Notas de autor
Henry F. López Cantorín es Contador Público (Universidad Nacional del Centro del Perú), Magíster en Gestión Pública (Universidad ESAN).
Rafael A. Cantorin Benites es Ingeniero Mecánico (Universidad Nacional del Centro del Perú), estudios concluidos de Maestría en Energía (Pontificia Universidad Católica del Perú), estudiante de maestría en Administración Pública y Gobierno mención Gerencia Pública Corporativa (Universidad Nacional del Centro del Perú).
Betzabeth R. Cantorin Benites es Bachiller en Arquitectura (Universidad Nacional del Centro del Perú), estudiante de maestría en Construcción mención Gestión y Organización de la Gestión (Universidad Nacional del Centro del Perú).
Diego Crisóstomo Huaringa es Bachiller en Educación, carrera profesional de Ciencias Matemáticas e Informática (Universidad Nacional del Centro del Perú).
rcantorin@uncp.edu.pe
